1.
1시간 소요.
점화식 세우는 아이디어는 금방 떠올라서 코드를 쭉쭉 써내려 갔다.
그러나 오답처리가 되어 질문 검색을 통해 반례를 찾아서 수정하는 데에 오랜 시간이 걸렸다.
점화식을 어떠한 식으로 세워야할 지 감을 잡았다는 점에서 만족한다.
2.
처음 풀었던 코드의 반례는 $2, 1, 5, 6, 7$ 이였다. 기댓값은 $20$ 인데, 나는 $19$ 가 나왔다.
$2$ 부터 선택하는 것이 최댓값인데 이를 고려하지 않았던 것이다.
dp배열은 해당 index 까지의 증가 부분 수열 합의 최댓값이다.
이해가 안 되면 다음을 명심하자.
DP문제는 큰 문제를 작은 문제로 쪼개어 생각하자
문제의 메커니즘은 완성된 dp배열을 보면서 설명하고자 한다.
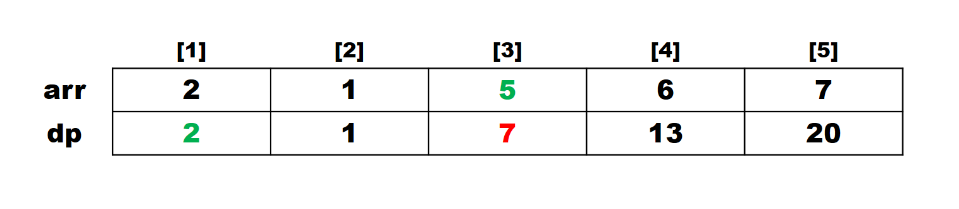
dp[3]을 계산하려면,
1. arr[3] 이전의 원소 즉 arr[2], arr[1] 원소가 arr[3]보다 작은 것을 찾는다. (증가하는 수열이므로)
2. 그러한 원소들 중 dp 배열의 원소가 가장 큰 값을 찾는다. (증가 부분 수열 중 최댓값을 찾기)
3.
import java.util.Scanner;
public class Main {
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = sc.nextInt();
}
int[] dp = new int[n + 1];
dp[1] = arr[1];
for (int i = 2; i <= n; i++) {
int max = 0;
for (int j = i - 1; j >= 1; j--) {
if (arr[i] > arr[j]) {
max = Math.max(max, dp[j]);
}
}
dp[i] = arr[i] + max;
}
int answer = 0;
for (int i = 1; i <= n; i++) {
if (dp[i] > answer) {
answer = dp[i];
}
}
System.out.println(answer);
sc.close();
}
}
4.
자신의 풀이를 설명한다는 것은 생각보다 어려운 것이었다..
'Algorithm' 카테고리의 다른 글
| [Java] 백준 1753 : 최단경로 (0) | 2020.08.12 |
|---|---|
| [Java] 백준 2468 : 안전 영역 (0) | 2020.08.12 |
| [Java] 백준 1541 : 잃어버린 괄호 (0) | 2020.08.11 |
| [Java] 백준 2217 : 로프 (0) | 2020.08.11 |
| [Java] 백준 1699 : 제곱수의 합 (0) | 2020.08.10 |
